勾股数的规律-勾股数的规律总结秒懂百科
在数学的世界中,勾股数是一个非常有趣的概念,它们是可以构成直角三角形的三组正整数。这些数字遵循着特定的规律,使得它们在数学中具有重要的意义。勾股数的规律不仅仅是数学中的一个小知识点,更是与古代数学家们的智慧和发现密切相关。从最著名的勾股数组合“3、4、5”到其他如“5、12、13”和“7、24、25”的组合,我们可以看到这些数字在直角三角形中的应用。
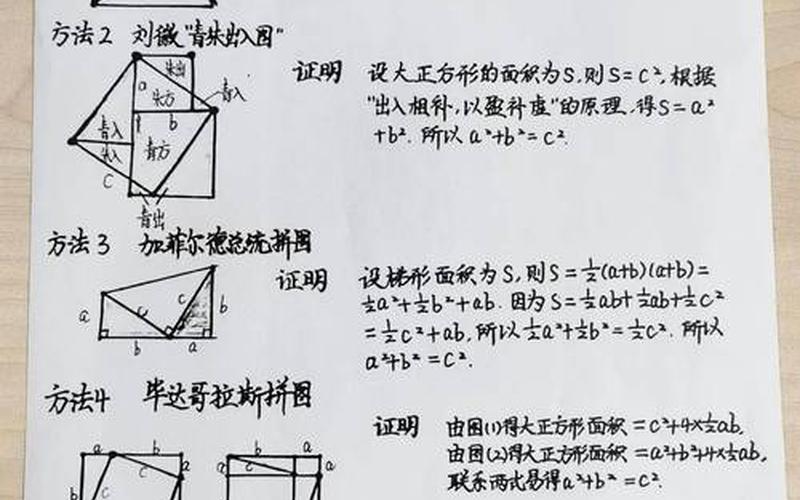
勾股数的概念源自古代中国和希腊的数学传统。在中国,直角三角形被称为“勾股形”,其中较短的直角边称为“勾”,较长的直角边称为“股”,斜边则被称为“弦”。这种命名方式反映了人们对这些数字的重视和理解。随着数学的发展,人们逐渐发现了勾股数的规律,并将其应用于各种数学问题中。
勾股数的定义和基本规律
勾股数是指能够构成直角三角形的三组正整数,它们满足勾股定理,即直角三角形两条直角边的平方和等于斜边的平方(a2+b2=c2。最著名的勾股数组合包括“3、4、5”和“5、12、13”,这些组合在历史上被广泛应用于建筑和测量中。
对于奇数勾股数,存在一个有趣的规律:当最小边为奇数时,其平方可以分解为两个连续正整数的和。,3的平方是9,可以分解为4和5,这样就形成了勾股数组合“3、4、5”。同样,5的平方是25,可以分解为12和13,形成“5、12、13”的组合。
勾股数的分类和生成规则
勾股数可以根据其性质分为互质勾股数和非互质勾股数。互质勾股数指的是三条边的最大公约数为1的勾股数,而非互质勾股数则是指存在一个大于1的公约数的勾股数。
对于偶数勾股数,规律与奇数不同。设A为偶数,则A的平方的一半可以分解为两个差为2的正整数,这样就可以得到B和C。,4的平方是16,16的一半是8,可以分解为3和5,形成“3、4、5”的组合。
勾股数的应用和意义
勾股数在数学和工程领域有着广泛的应用。它们不仅用于建筑设计和测量,还被用于解决三角形问题和计算距离。在计算机科学中,勾股数也被用于算法设计和优化问题。
除了数学应用外,勾股数还体现了数学的美和规律性。通过研究勾股数,我们可以更深入地理解数学的基本原理和模式。这种理解有助于我们在解决复杂问题时找到更有效的方法。
勾股数的历史和文化意义
勾股数的历史可以追溯到古代文明,如中国和希腊。在中国,勾股数被用于《九章算术》等古代数学著作中。这些数字不仅是数学工具,也反映了古代数学家们对自然世界的观察和理解。
在文化方面,勾股数也被视为智慧和创造力的象征。它们代表了人类对数学规律的发现和应用,这种发现使得我们能够更好地理解和改造世界。
总结和展望
勾股数的规律和应用为我们提供了一个丰富的数学世界。通过研究这些数字,我们不仅可以深入理解数学的基本原理,还可以在实际问题中找到灵感和解决方案。随着数学的发展,勾股数将继续在各个领域发挥重要作用。
相关内容的知识扩展:
1. 费马大定理与勾股数
费马大定理指出,对于任何整数n>2,方程an+bn=cn。虽然费马大定理与勾股数没有直接关系,但它们都体现了数学中关于整数解的探索和发现。
2. 勾股数在计算机科学中的应用
在计算机科学中,勾股数可以用于优化算法和解决几何问题。,在计算机图形学中,勾股数可以帮助计算距离和角度,提高图形渲染的效率。
3. 勾股数与其他数学概念的联系
勾股数与其他数学概念,如三角函数和圆的性质,有着密切的联系。通过研究勾股数,我们可以更好地理解这些数学概念,并在实际问题中找到应用。
4. 勾股数的文化意义
在文化方面,勾股数代表了人类对数学规律的追求和发现。它们不仅是数学工具,也是智慧和创造力的象征。在教育中,勾股数可以帮助学生更好地理解数学的美和规律性。
5. 勾股数的历史发展
勾股数的历史可以追溯到古代文明,如中国和希腊。在这些文明中,勾股数被用于建筑和测量,并在数学著作中得到广泛应用。随着数学的发展,勾股数的应用和研究也在不断扩展。
参考文献
- CSDN博客:关于勾股数的规律及证明原创
- 百度百科:勾股数
- 喜马拉雅:勾股数的规律
- 维基百科:勾股定理
- 百度知道:勾股数有哪些规律
- 全球快报:勾股数的规律总结视频
- 360Doc:学好勾股数的这3个重要规律和公式
- 百度百科:勾股定理